Finite-difference on non-uniform grids

The central-difference schemes for computing derivatives on a uniform grid are very well-known. They are derived from the Taylor series expansion of a function. An infinitely differentiable function, \(f(x)\), can be written as a series between two points \(x = a\) and \(x = b\) as below:

$$ f(b) = f(a) + f'(a)(b - a) + \frac{f''(a)}{2!}(b - a)^2 + \frac{f'''(a)}{3!}(b - a)^3 + ... $$

The points \(a\) and \(b\) are really close to each other such that we can write \(b = a + h\), where \(h\) is a very small value. So we can rewrite the above series as below:

$$ f(b) = f(a) + f'(a)h + \frac{f''(a)}{2!}h^2 + \frac{f'''(a)}{3!}h^3 + ... $$

Since \(h\) is a really small number (\(h \ll 1\)), terms like \(h^2\), \(h^3\) etc tend to be extremely small and can be neglected as an approximation. This yields the first-order approximate forward finite-difference formula for calculating the derivative of a function:

$$ f'(a) = \frac{f(b) - f(a)}{h} $$

The above formula is called forward difference since it uses a point (\(x = b\)) ahead of the point of interest (\(x = a\)) for evaluating the derivative. If instead we take a point \(x = c\) behind \(x = a\) such that \(c = a - h\), the corresponding expansion would be:

$$ f(c) = f(a) - f'(a)h + \frac{f''(a)}{2!}h^2 - \frac{f'''(a)}{3!}h^3 + ... $$

Subtracting the expansions for \(f(b)\) and \(f(c)\) gives an interesting outcome:

$$ f(b) - f(c) = 2 f'(a)h + 2 \frac{f'''(a)}{3!}h^3 + ... $$

What is interesting about the above result is that the \(h^2\) term got cancelled. As a result, evaluating \(f'(a)\) from the above equation is second-order accurate in the sense that errors are of the order \(h^3\) and above only. This gives the second-order central difference formula for evaluating derivatives:

$$ f'(a) = \frac{f(b) - f(c)}{2h} $$

These are fundamental building blocks of finite-difference solvers for partial differential equations. Typically the domain over which the derivatives are calculated is divided into a fine and uniform grid with a spacing \(h\) as above, and this allows one to compute the derivative of the function at every grid point if we know the values of the function at all these points.

All of these are fairly straightforward and available in a plethora of resources. Why I am writing this post (it is also a reference for my use later) is to derive and store the corresponding formula for non-uniform grids. Sometimes I need to evaluate derivatives on such grids and for some reason, a Google search for the below formula turns up nothing useful for me. Invariably I spend some time re-deriving the formula, which isn't terribly exhausting, but tiresome nevertheless.

Now we don't have a constant spacing \(h\). Rather, we have \(b = a + h_r\) to the right of \(a\), and \(c = a - h_l\) to the left of \(a\). To simplify things, introduce a grid stretching ratio \(\beta\), and we end up with the following equations after removing the \(h^3\) terms:

$$ f(b) = f(a) + f'(a)h_r + \frac{f''(a)}{2}h_r^2 + ... $$ $$ f(c) = f(a) - f'(a)h_l + \frac{f''(a)}{2}h_l^2 - ... $$ $$ \beta = \frac{h_r}{h_l} $$

Now I am a little lazy when it comes to doing such algebra. So we have a short Python code using the sympy module to encode the above equations like below:

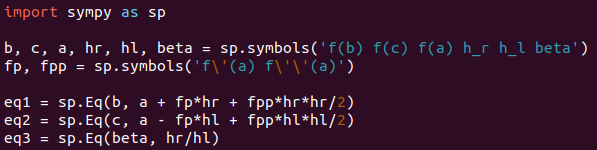
The above equations can be solved for \(f'(a)\), \(f''(a)\), eliminating \(h_l\) in the process. This is done using the sympy.solve function.

Since the focus here is on the first derivative, only the first component of the result is printed.

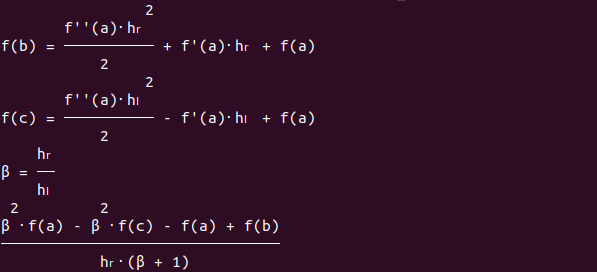
The last line in the output above gives the required stencil for non-uniform grids:

$$ f'(a) = \frac{-\beta^2 f(c) + (\beta^2 - 1) f(a) + f(b)}{h_r(\beta + 1)} $$

Usually finite differences are written out on grids with an index \(i = 1, 2, 3 ... N\). Therefore \(f(a)\), \(f(b)\) and \(f(c)\) are usually written in their indexed forms as \(f_i\), \(f_{i+1}\) and \(f_{i-1}\) respectively. So the final form which can be quickly coded in when needed would look like:

$$ f_i' = \frac{-\beta^2 f_{i-1} + (\beta^2 - 1) f_i + f_{i+1}}{h_r(\beta + 1)} $$

Caveat emptor! This is not a respectably accurate formula and is best used for quick and approximate calculations. More accurate compact schemes are available if actual numerical simulations need to be performed on such non-uniform grids without grid transformations.